古典積層理論(ゆるふわ)
ふんわり古典積層理論についてまとめます。
今回は、炭素繊維がM40Jのプリプレグを使用して積層板を作成し、物性を決定していきます。
購入したプリプレグ(一方向強化材)を積層していく流れを図1に示します。
図1▼
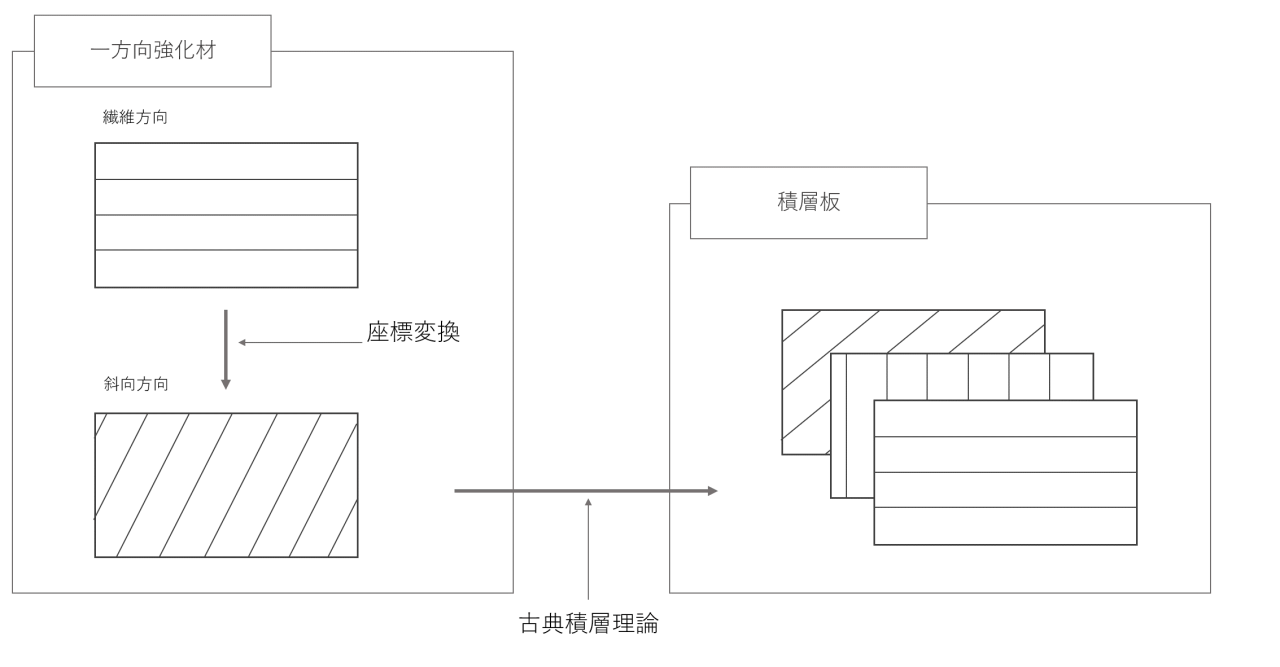
基本的にプリプレグなどの物性は調べれば出てきます。
Toray Composite Materials▶https://www.toraycma.com/page.php?id=661
今回繊維方向を1、直交方向を2と座標指定します。
図2(こんな感じ)▼
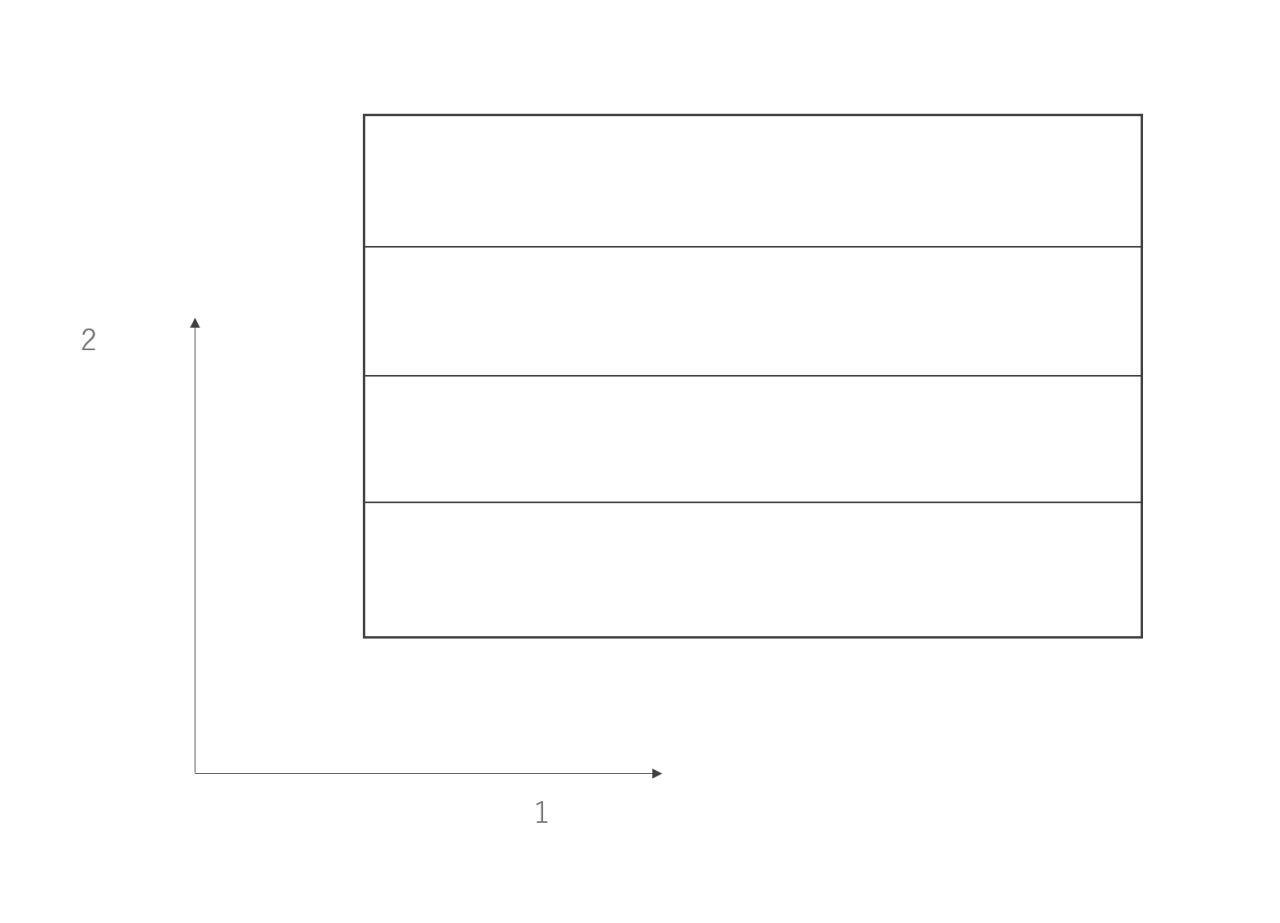
そうした際の初期物性を下の表にまとめます。
図3(物性表)▼
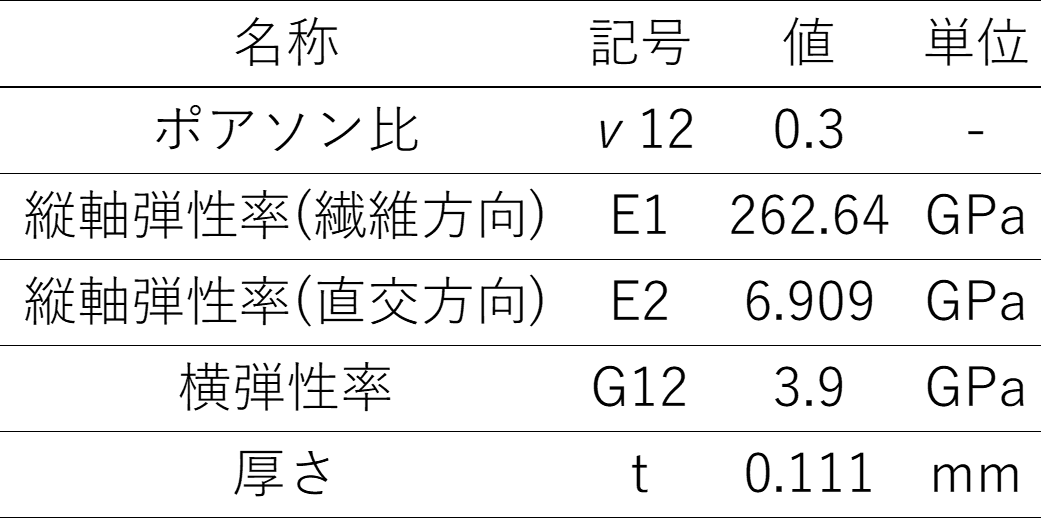
一般に繊維強化複合材は、方向によって弾性率が異なる異方性材料(anisotropic material)です。
普段よく出会う金属やプラスチックなどの材料は、どの方向に引っ張っても同じように変形する材料で、等方性材料(isotropic material)と言います。
図4(等方性材料を引っ張ったとき)▼

等方性材料の場合ポアソン比ν、縦弾性率E、横弾性率Gとして
応力とひずみの関係はこんな感じであらわされます。
式⑴▼
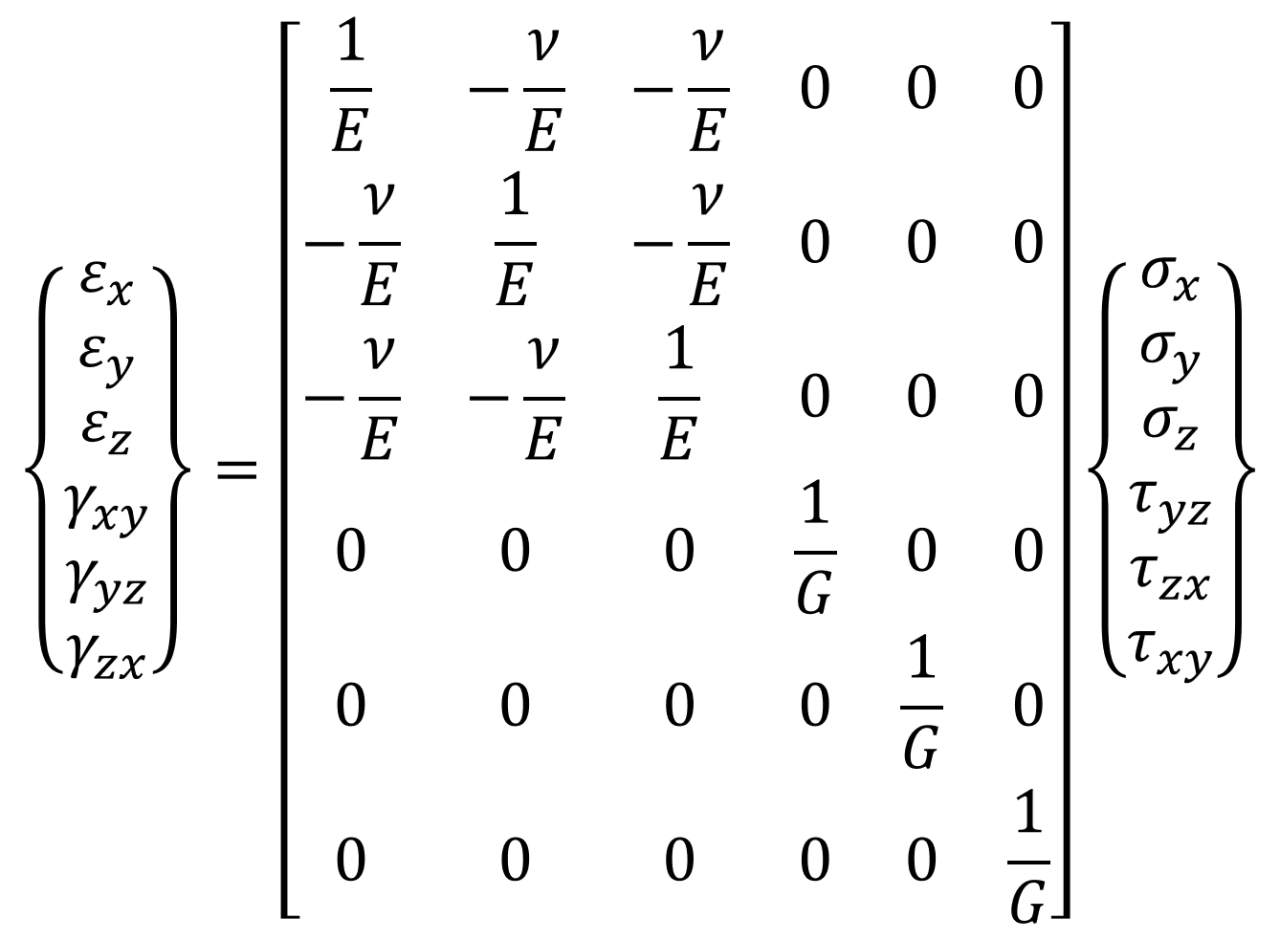
よく材力の教科書とかで見る感じですね。
異方性材料はどうなるかというと、剛性係数(stiffness coefficient)Qを導入して表します。
式⑵▼
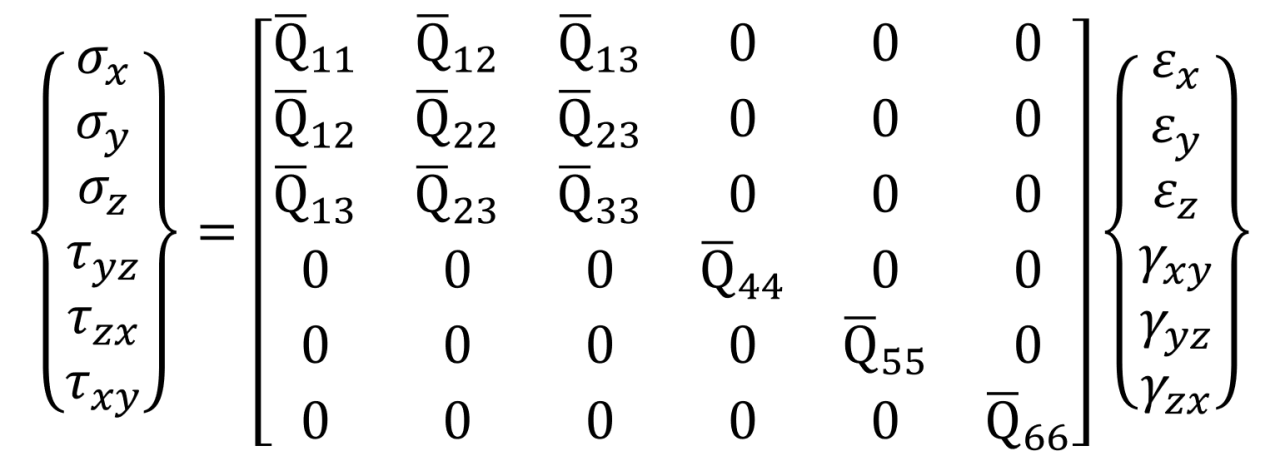
今回は積層板を考えているので、x,y方向だけの2次元で表せます。
式⑶▼
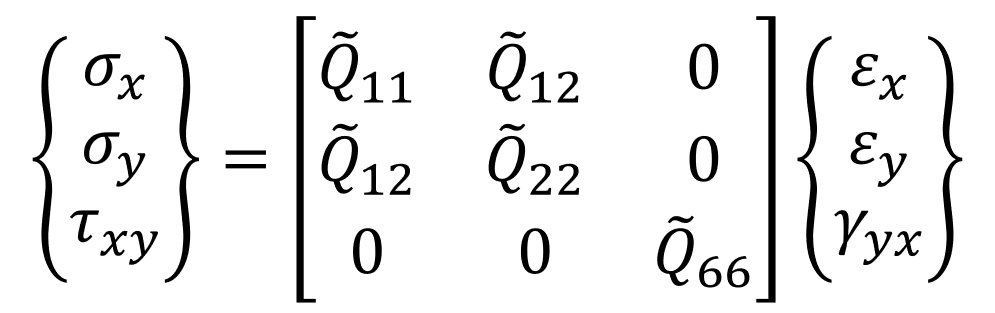
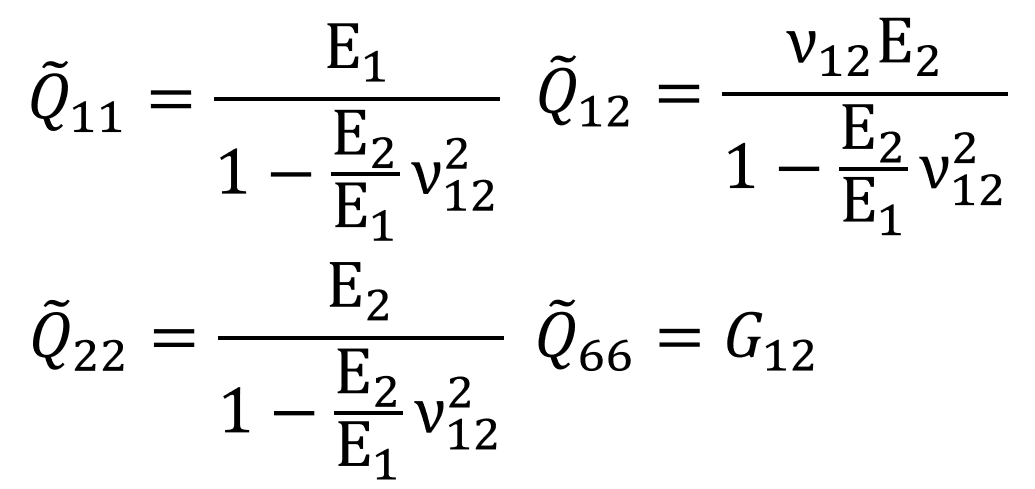
これが基本式になります。
次に、プリプレグを回転させた状態の物性を求めます。
図5(θ回転させた状態のプリプレグ)▼
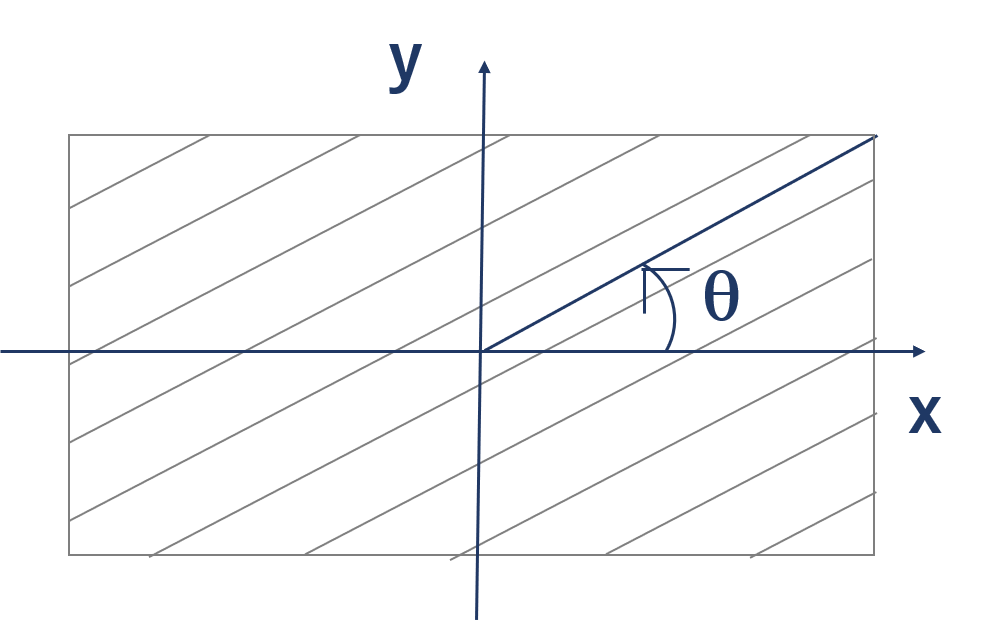
与えられた物性は繊維方向と直交方向のデータしかありません。与えられた物性を用いて応力とひずみの関係を導くために、l=cosθ、m=sinθとして、材力的座標変換をします。変換後の座標を1,2とします。
( 力学的座標変換とは違い、回転後に面も移動しているます。)
ごちゃごちゃ計算してまとめた回転後の式を示します。
式⑷▼
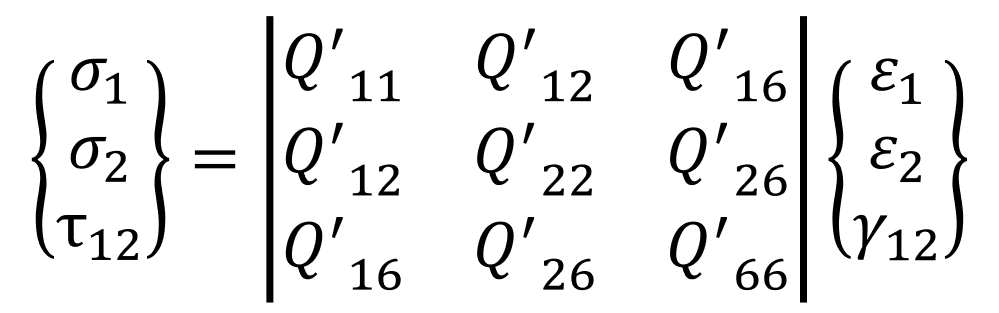
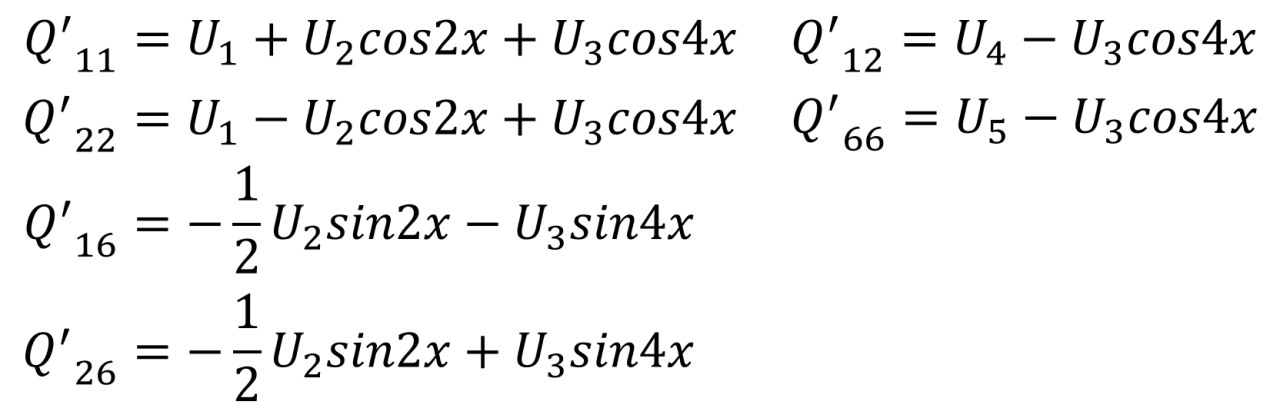
新しく弾性不変量Uを導入しました。 これが回転後の式です。
Q’のパラメータは横軸を角度として下の図のように変わります。0度の際はQ'16とQ'26が0になり、式⑶と一致します。
図6(Q'パラメータの変化)▼
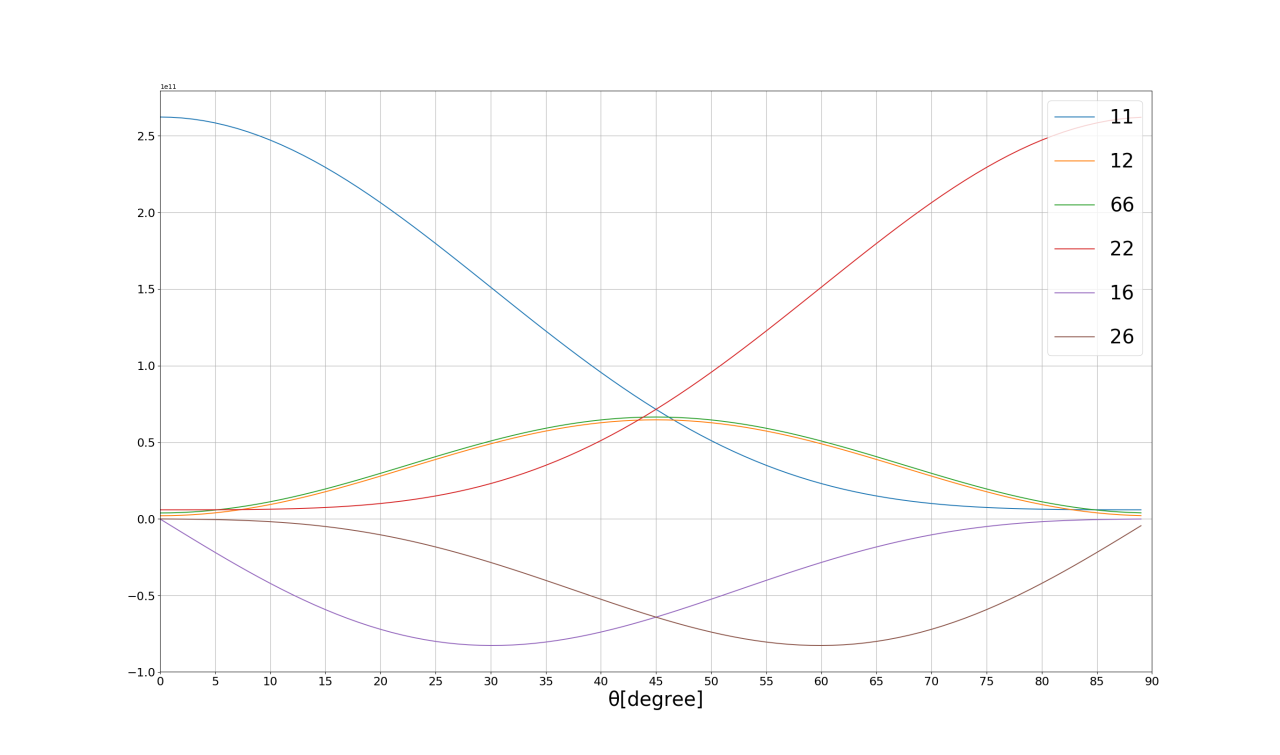
θ=0以外の際は、Q'の6つのパラメータが値を持ちます。式⑶との比較からもわかるように、プリプレグを回転させることで、加えられた応力によりせん断変形を生じます。
試しに、θ=45°で、σx=4.0[GPa]で引っ張ります。
図7(変形図)▼
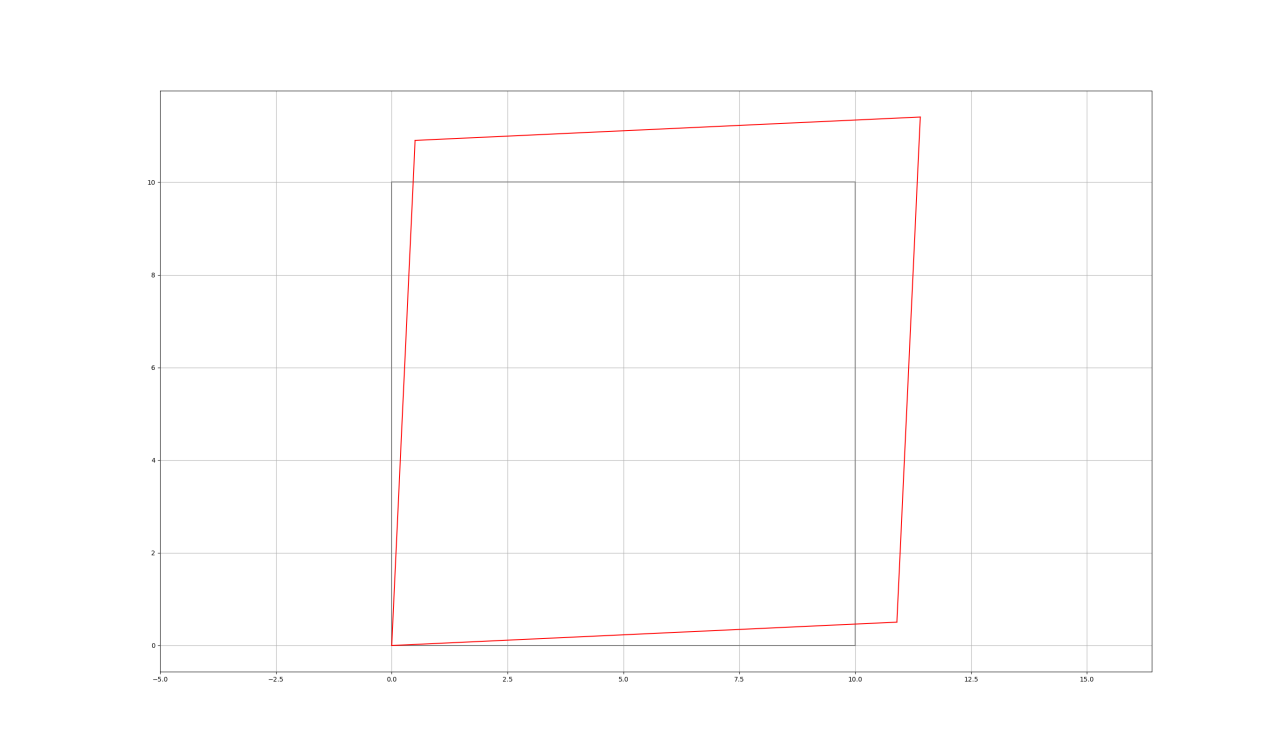
グレーは変形前、赤が変形後です。
せん断変形していることが良く分かります。
一方向強化材は強化方向には強いけど、直交方向には非常に弱いです。そこで、一方向強化材を様々な方向に回転させ、それを重ね合わせることで、 用途に合った物性を獲得できます。設計できる材料と呼ばれる所以です。(?)
「板厚方向の中央面に垂直な線要素は変形後も変形した中央面に垂直である」というキルヒホッフの仮説を用いて、変位分布を簡単化します。
図8(平面図)▼
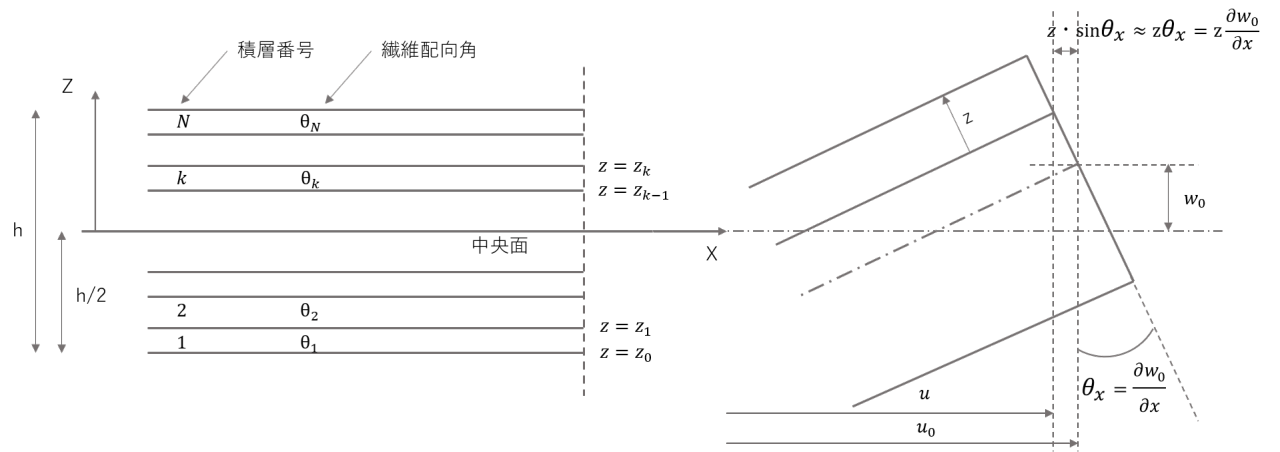
図9(作用する力)▼
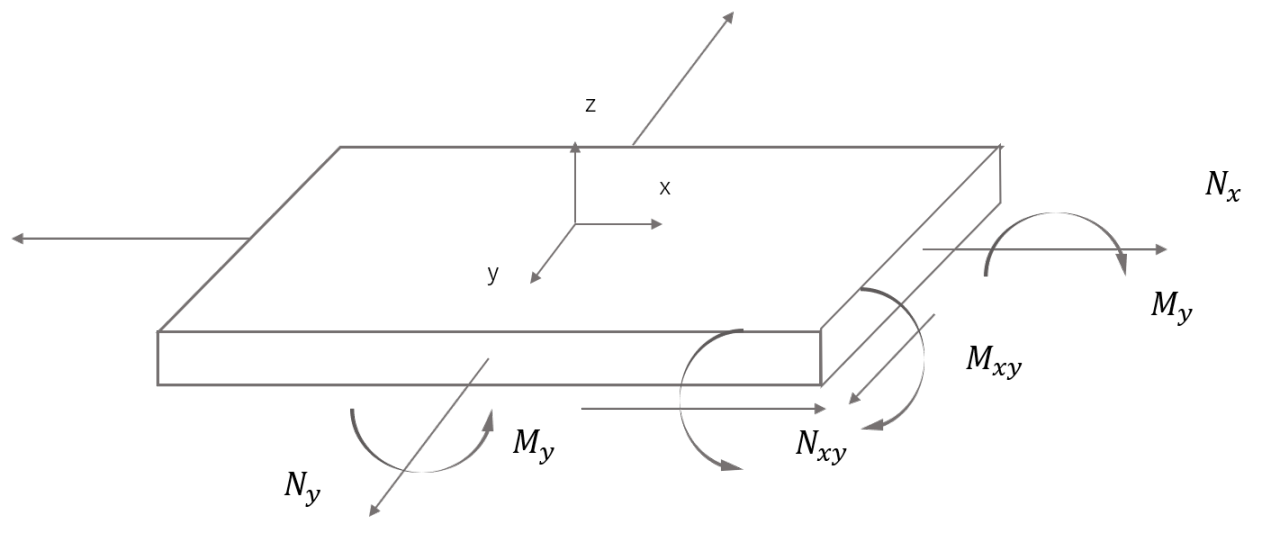
中央面のひずみ、中央面の曲率、ねじり率を用いて作用する力NとMとの関係式を式⑸に示します。
式⑸▼
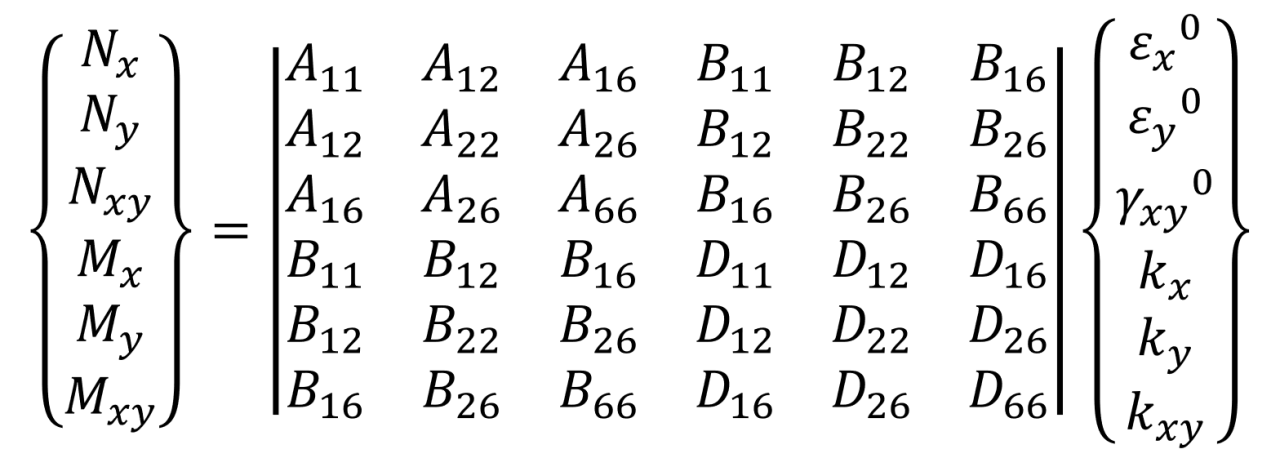
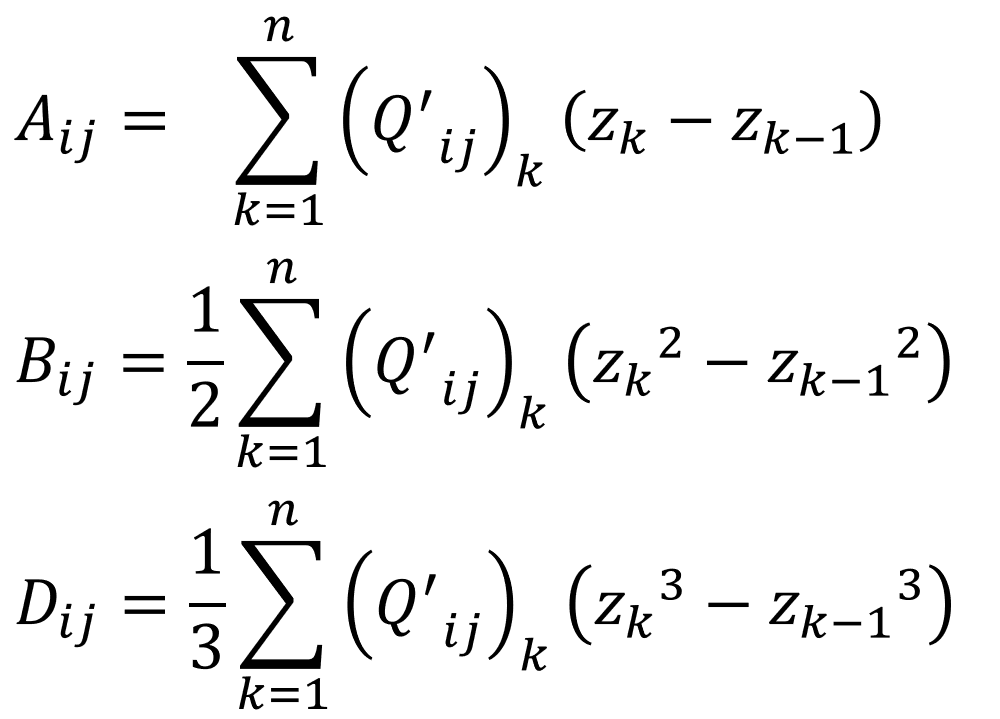
とこうなります。これを古典積層理論といいます。
例えば、Nxについてみてみます。
図10(Nxについて)▼
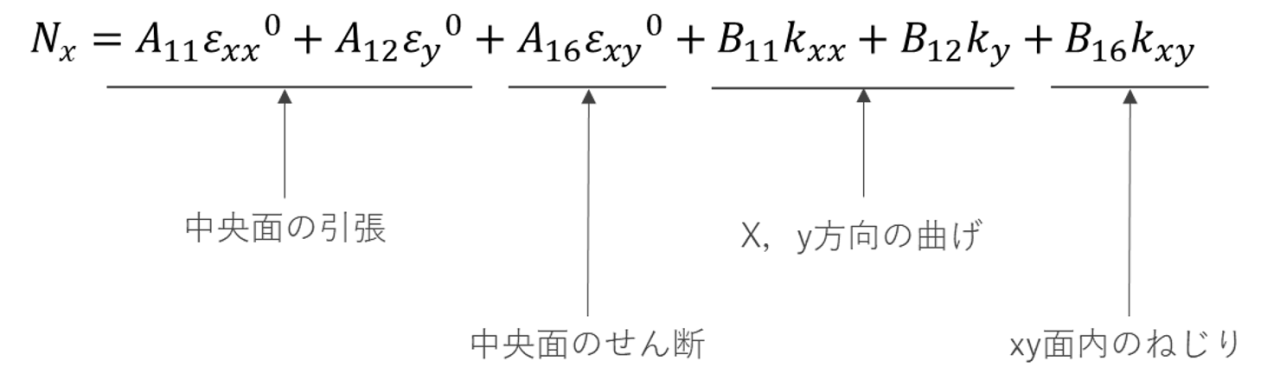
引張荷重を加えると
ひずみだけではなく、曲率 が生じます。
こんな感じに加えた力に対して、様々な変形が生じます。
図11(変形例)▼
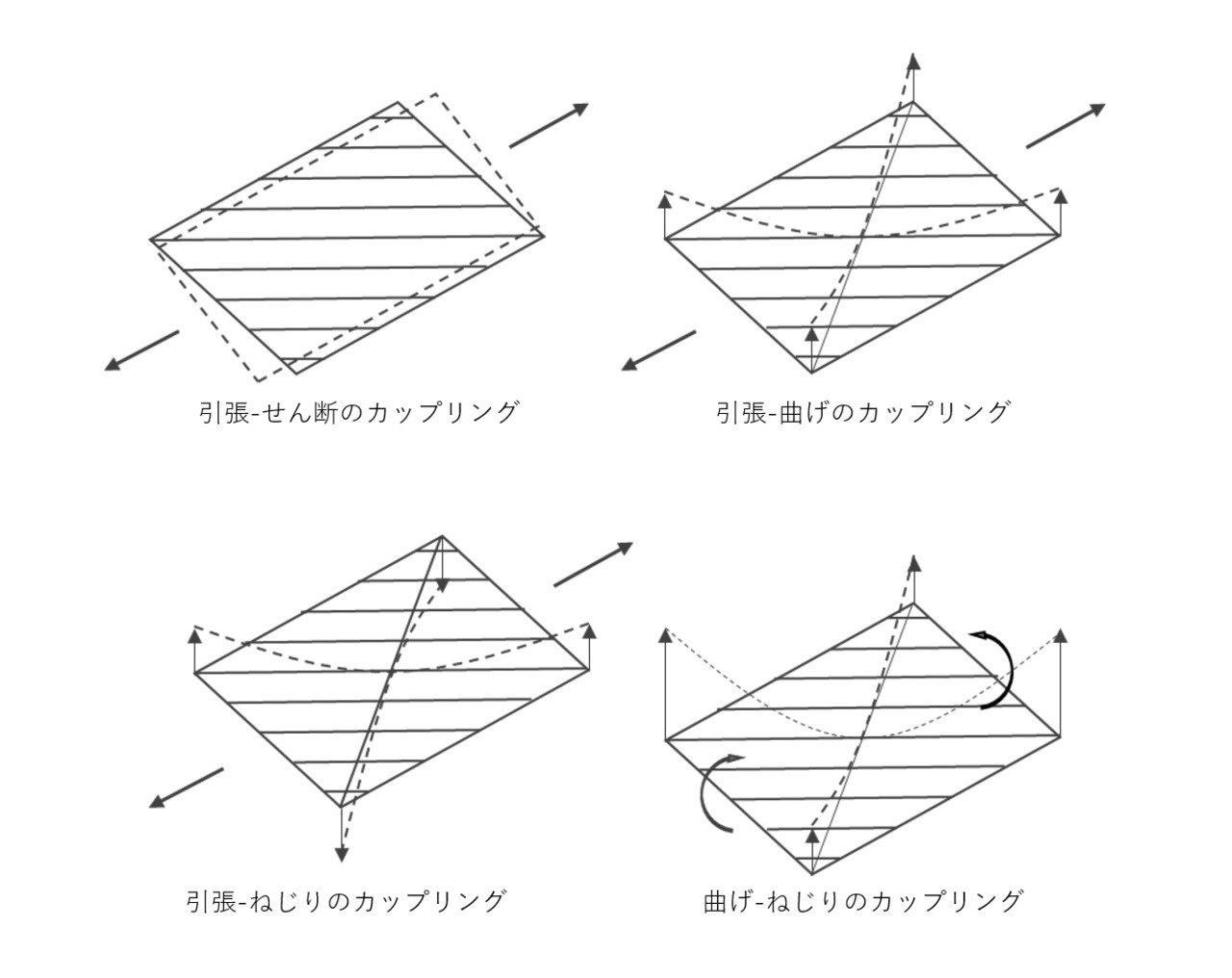
ここから、様々な積層板についてみていきます。ある条件を満たすことで式⑸をより簡単に扱うことができます。
調和積層板
-θの層がn/2層、θの層がn/2層ある積層板(すべて層の厚さは同じ)
そうするとA26 =0になります。
(
引張-せん断のカップリングが発生しなくなる。)
対称積層
中央面を基準面として対称な位置に同じ位置の繊維角の層が存在する積層板
図12(対称積層積層図)▼
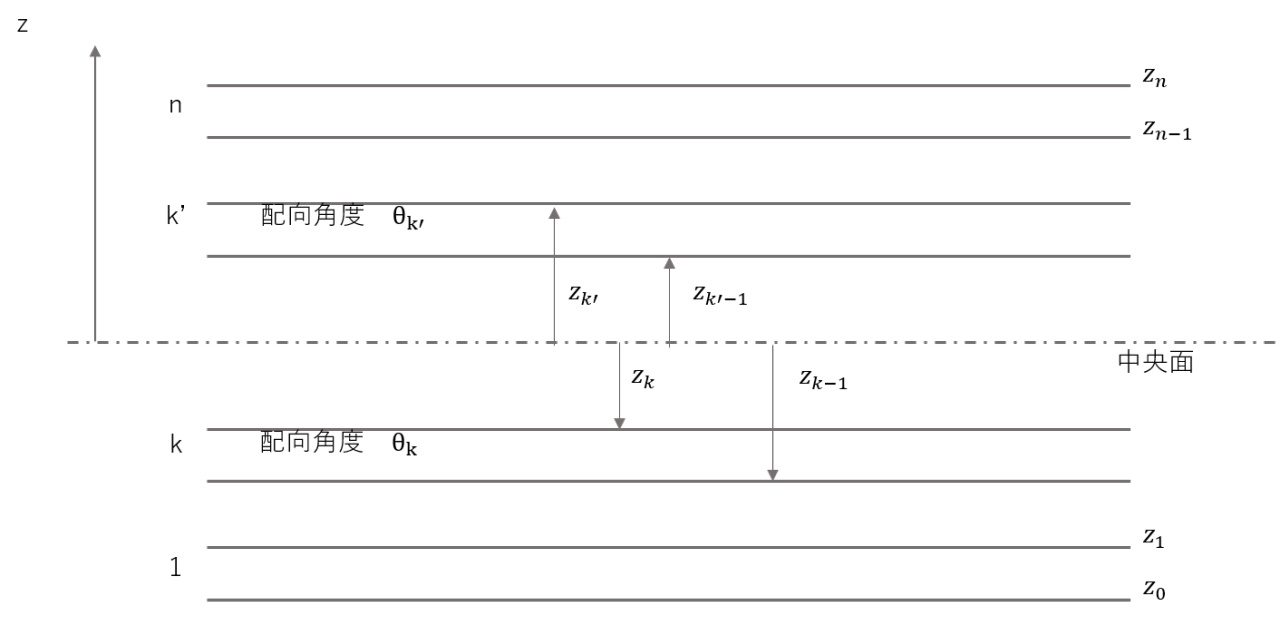
そうするとなんとBij=0になります!
そうすると式⑸はすごく扱いやすくなります。
式⑹▼
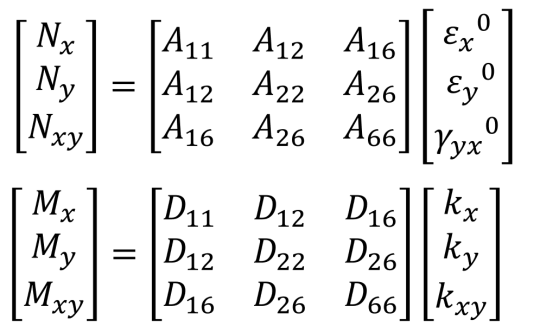
式⑹を使って積層板の物性を決定します。
よく[0/90/45/-45/90/0]の6層単位の積層板 を使います。
これは調和積層かつ対称積層です。これを用いた12層積層板を計算するとこうなります。
Amatrix
| +150848849773.6245 +30565500590.7643 -0.0000
| +30565500590.7643 +150848849773.6245 -0.0000
| -0.0000 -0.0000 +32992912295.7150
Bmatrix
| -0.0000 -0.0000 +0.0000
| -0.0000 +0.0000 +0.0000
| +0.0000 +0.0000 -0.0000
Dmatrix
| +26021244067.7562 +3605835615.7577 -1051726932.5393
| +3605835615.7577 +20412033760.8797 -1051726932.5393
| -1051726932.5393 -1051726932.5393 +3964733291.1580
得られたAとDを用いて、一軸応力状態(σx=σ0)や(τxy=τ0)を考えることで縦弾性率、横弾性率、ポアソン比を得られます。
Ex [Pa] : 117899500121.90343
NUxy [ ] : 0.2026233586575788
Gxy [Pa] : 26890412801.47911
すごく省略パラダイスでしたが、こんな感じで物性を決定していきます。
是非興味持ったかたは参考文献等の方が全然わかりやすいので読んでみてください!!
参考文献
入門複合材料の力学 培風館(2009)
末益 博士
複合材料力学入門 第1章 複合材料力学のための弾性学、材料力学の基礎
福田 博
構造解析技術者のための複合材料入門(1)複合材料の概要と力学的特性(直交異方性材料の力学) Mechanical CAE NEWS Vol.26
平山 紀夫
複合材料力学入門 第3章 積層板の理論と最適設計の基礎
福永 久雄